
Rd Sharma Class 12 Solutions Chapter 6 Determinants Updated For 22 23
X `y/2 = 1/2`Cramer’s Rule is a pretty nifty tool to use to find solutions to a system of equations We will see some examples as well as one with $ 3 $ variables Example 1 Solve the system of equations shown below using Cramer’s Rule $ \begin{align*} { – x } – y &= \,
2x 3y=2 x-y/2=1/2 by cramer's rule
2x 3y=2 x-y/2=1/2 by cramer's rule-Cramers rule for 2x2 Use Cramers rule to solve the system of 2 linear equations for 2 unknowns as shown below x2y=3 x2y = 3 2x3y=1 2x3y = 1 Equation 6 System of 2 linear equations for 2 unknowns We convert the system into an augmented matrix Equation 7 Augmented matrix for the 2x2 system How do you solve the following system using Cramer's rule #2xy=3, 4x3y=5#?
How To Use The Gauss Jordan Inverse Method To Solve The Linear Equations Of These Three Unknowns 5x 6y 7z 40 2x 4y 2z 34 X 3y 5z 30 Quora
Find k if the equations 2x 3y – z = 5;Free PreAlgebra, Algebra, Trigonometry, Calculus, Geometry, Statistics and Chemistry calculators stepbystepLet’s have a look at the formulas of Cramer’s rule for 2×2 and 3×3 matrices Cramer’s Rule 2×2 Cramer’s rule for the 2×2 matrix is applied to solve the system of equations in two variables Let us consider two linear equations in two variables a 1 x b 1 y = c 1 a 2 x b 2 y = c 2 Let us write these two equations in the form of AX = B
Answer (1 of 3) I will just describe the process to find x, y & z using Cramer Rule Make a determinant of all coefficients of variables and call it ∆ 2 1 1 3 0 1 = ∆ 4 5 2 Replace coefficient of x in ∆ with constants on RHS and call it ∆x 3 1 1 2 0 1 = ∆x 1 5 2Steps for Solving Linear Equation 2x3yz=0 2 x 3 y − z = 0 Subtract 3y from both sides Anything subtracted from zero gives its negation Subtract 3 y from both sides Anything subtracted from zero gives its negation 2xz=3y 2 x − z = − 3 yClick here👆to get an answer to your question ️ Solve by Cramer's Rule x y z = 2, x 2y z = 1 and 3x y 5z = 4
2x 3y=2 x-y/2=1/2 by cramer's ruleのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 2 | 2 |  2 |
2 |  2 | 2 |
 2 |  2 |  2 |
 2 |  2 | 2 |
 2 | 2 | 2 |
 2 |  2 | 2 |
 2 |  2 |  2 |
 2 | 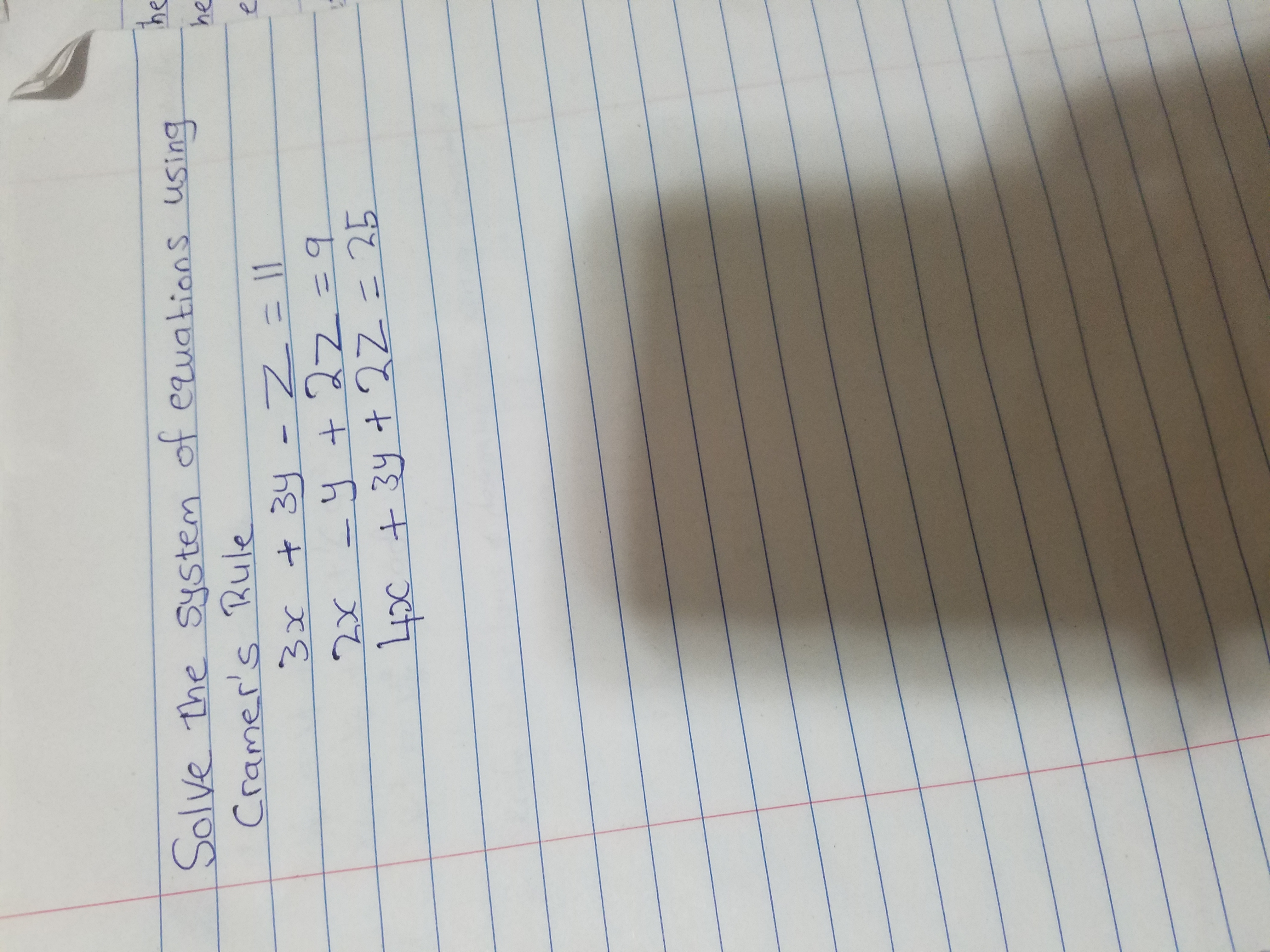 2 |  2 |
 2 |  2 |  2 |
 2 |  2 |  2 |
2 |  2 |  2 |
 2 |  2 | 2 |
 2 |  2 | 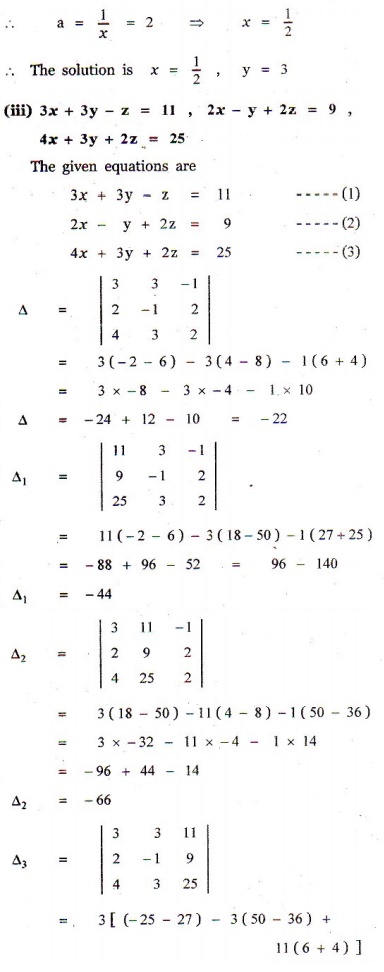 2 |
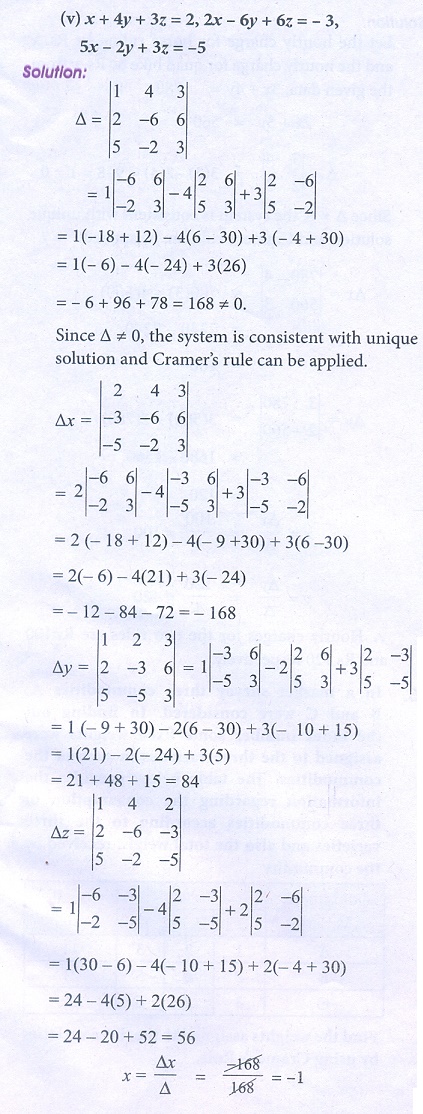 2 |  2 | 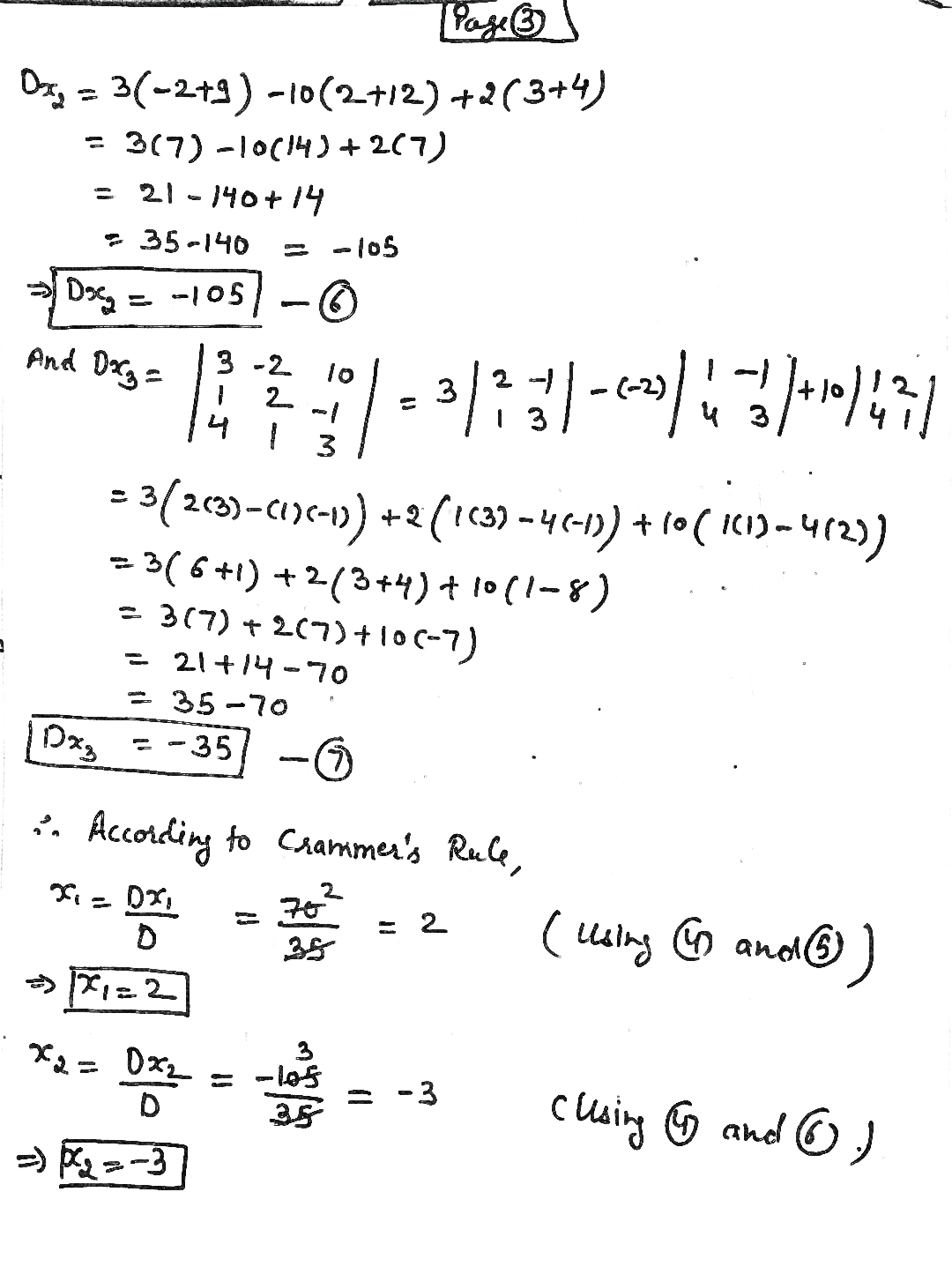 2 |
 2 |  2 |  2 |
 2 |  2 |  2 |
 2 | 2 | 2 |
 2 | 2 |  2 |
 2 | 2 |  2 |
 2 |  2 |  2 |
 2 |  2 | 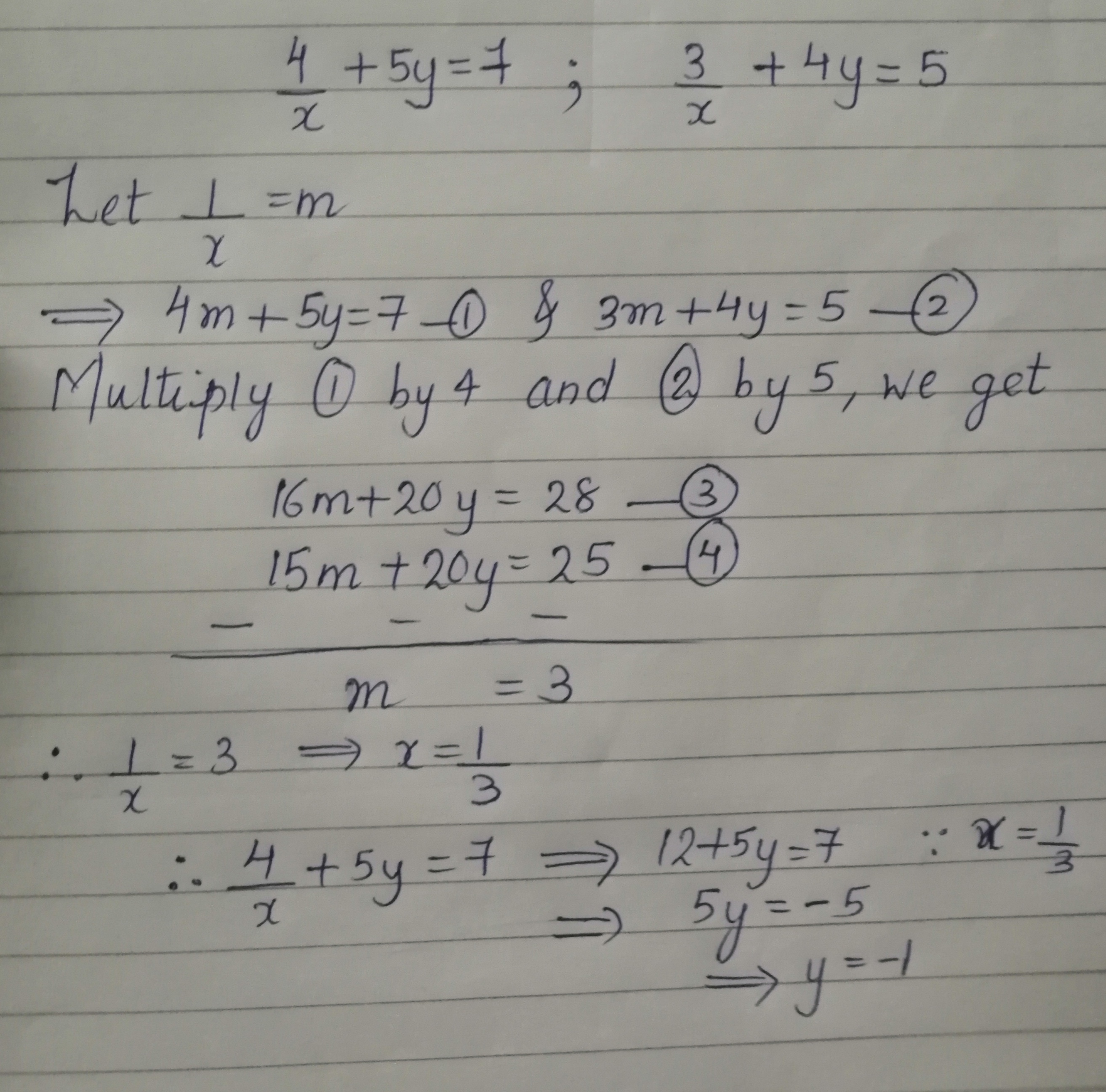 2 |
 2 |  2 | 2 |
2 |  2 | 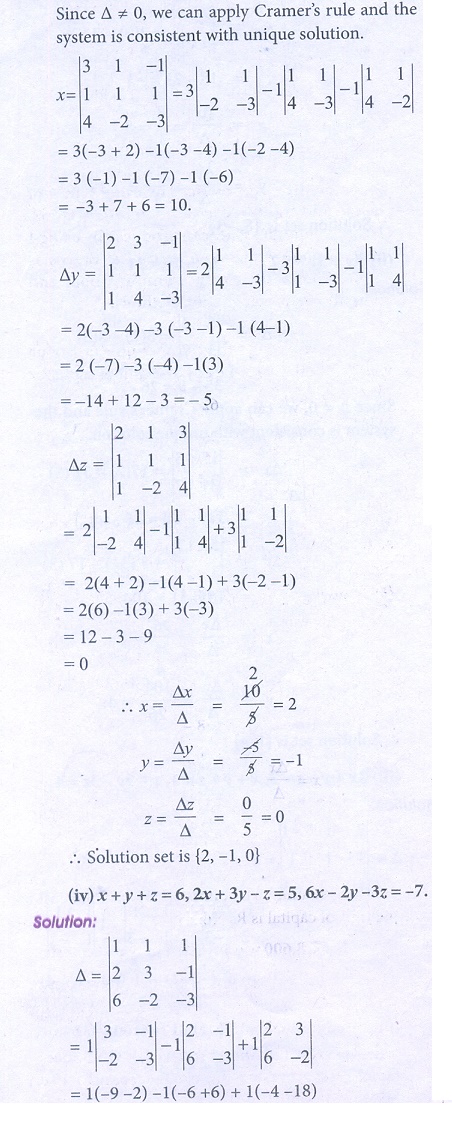 2 |
 2 |  2 |  2 |
 2 |  2 |  2 |
 2 | 2 |  2 |
 2 | 2 |  2 |
 2 | 2 |  2 |
 2 |  2 |  2 |
 2 | 2 |  2 |
 2 | 2 |  2 |
2 |  2 |  2 |
2 | 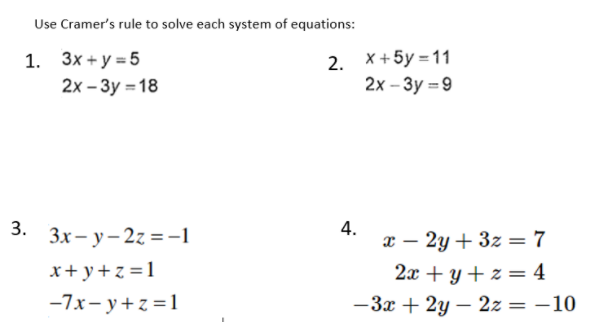 2 |  2 |
2 |  2 |  2 |
 2 |
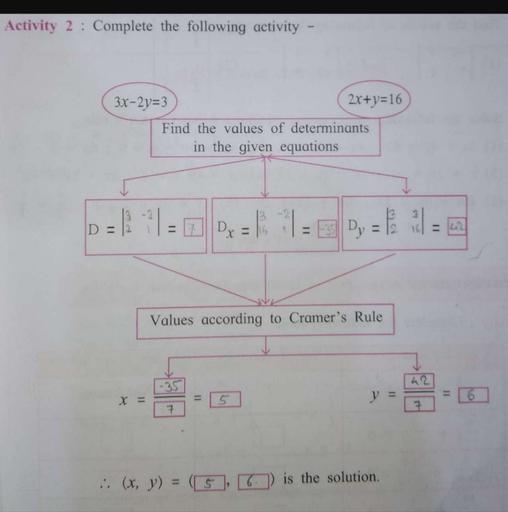
vi 2x 3y = 2 ;Solve the following simultaneous equations using Cramer’s rule 2x 3y = 2;





0 件のコメント:
コメントを投稿